We can no longer use the binomial distribution probability formula in such an instance. Logically, the answer to that challenge is p = ½ = 0.5. The single-zero roulette game has 37 possible cases (36 numbers, plus 0). The double-zero roulette game has 38 possible cases (36 numbers, plus 0, plus 00). The odds vary with the type of bet. To calculate the odds for winning with a given roulette bet, you need to figure out what its probability is. Then you can use the following formula: Odds for Winning = Probability of Winning / (1 – Probability of Winning). Here is how you should do the roulette probability formula: P(Red) x A (value for red) + P(Not red) x A (value that is not red) = 18/37 + 2 + 20/37x (-1) = 0.4865. Interpreting the results of the probability roulette calculator. Using the probability mass function and summation notation allows us to more compactly write this formula as follows, where the summation is taken over the index i: E( X ) = Σ x i f ( x i ). This version of the formula is helpful to see because it also works when we have an infinite sample space.

1. Roulette Probability Formula Solver
2. Roulette Probability Formula Cheat

I have noticed on the internet there are people selling ‘systems’ or ‘strategies’ which they claim can be used to overcome the odds and win at roulette. Unfortunately, it is mathematically impossible for any of these systems to work. Many people still don’t understand the basic probability of roulette, and the fact that each new spin of the wheel has independent odds.

A casino has an edge over anyone who plays roulette (generally 5.26% on an American style table). Because of this, the odds of coming out in front in the long-run are very very small, and close enough to impossible. If a player bets $1 on red or black on an American table (with 0 and 00) there is a probability of 18/38 (47.3%) of winning $1. The house advantage lies in the fact that 2 of the 38 squares (0 and 00) are not red or black. To many people, the odds seem close enough to 50/50, but even with this small edge, the casino will make a good profit over time.

Roulette Probability Formula Solver

The more bets you make the more the house edge works against you. If you bet on every number (all 38) at once, you can see that the payoff for being right (35 to 1) is not enough to compensate the cost of placing all the bets.

Gambling games and trading systems are similar in that a system with a negative expected return can not be traded profitably regardless of the strategy used. ie, it doesn’t matter how much you bet each time or how you change your bet size on each turn, the house advantage will remain. Albert Einstein apparently said: “You cannot beat a roulette table unless you steal money from it.”

I have made a spreadsheet which allows you to play roulette with real odds, and you can also test the outcome of any bet or combination of bets. For example, here is a screen shot of the outcome of starting with $1,000 and betting $50 on black, $50 on column 2 and $20 on number 3 simultaneously. This bet is repeated 1,000 times. On this run it actually did pretty well initially, increasing to around $5,000 after a few hundred games, but eventually, the house edge worked against it and it finished with a loss of $4,690. Of course, if you repeated this process you would get a different outcome, but you would still expect to lose after many repetitions of the bet. Very occasionally you would end up with a profit after running the 1,000 bets, however, if you repeat this exercise many times you will see how rare that is.

My best result so far was turning $1,000 into $90,000 (fictional) dollars before seeing that amount quickly plummet back to $0.

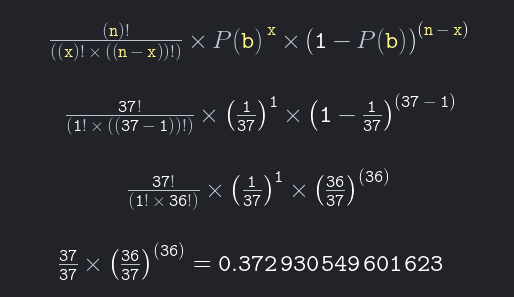
Roulette Probability Formula Cheat

Please try out my spreadsheet (you will need to enable macros in Excel) and leave a comment with any questions, ideas or high scores!